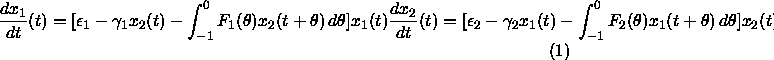
The purpose of this note is to give an impression of some of the research in the project operator theory and applications which focuses on operator theoretical methods for analyzing problems arising from concrete classes of integral, differential and difference equations.
In the study of predator-prey models and viscoelasticity, Volterra [8] formulated some general differential equations incorporating the past states of the system:
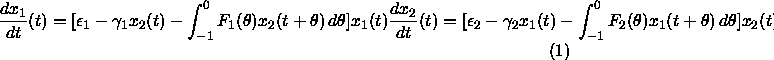
In this model, it is assumed that the solution 
is given on the interval [-1,0] and satisfies equation (1) for
.
This system is an example of a retarded functional differential equation. Systems of this type appear in a number of interesting applications, i.e., biology, economics, feedback control and number theory.
To understand the qualitative behaviour of the solutions of eq. (1) near an equilibrium, a thorough understanding of the corresponding linearized equation is needed, that is, an equation
where 
is an 
-matrix valued function of bounded variation
(in the specific example n=2).
The initial data is given by 
for 
, where
is a given continuous function on [-1,0] with values in 
.
The solution with initial data we shall denote by 
,
, where C denotes the space of -valued continuous
functions on the interval [-1,0] provided with the sup-norm.