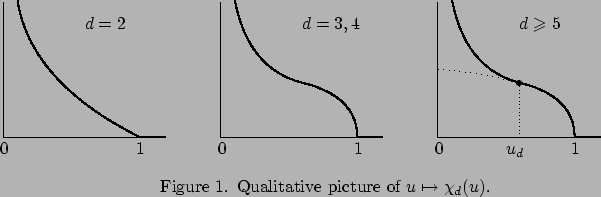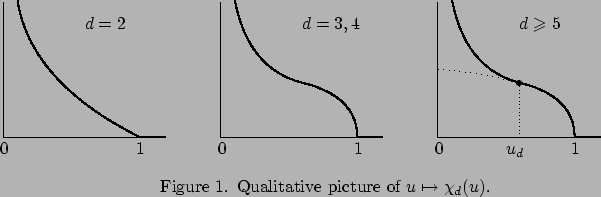

Next: References
Up: Fluctuations of the Wiener
Previous: Moderate deviations
A closer analysis of (7-8) reveals a number
of surprises. First, the 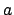 -dependence can be removed by Brownian
scaling. This gives (recall that
-dependence can be removed by Brownian
scaling. This gives (recall that
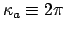 for
for
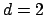 )
)
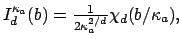 (10)
(10)
where
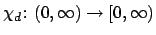 is given by
is given by
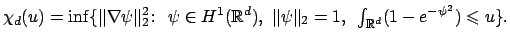 (11)
(11)
Next, the variational problem in (11) displays the
dimension dependence shown in Figure 1.
In this figure 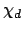 has an infinite slope at
has an infinite slope at 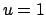 when
when
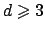 ,
showing that the connection with the central limit theorem is
anomalous. Moreover,
,
showing that the connection with the central limit theorem is
anomalous. Moreover, 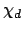 has a non-analyticity at
has a non-analyticity at
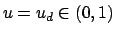 when
when
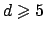 , playing the role of a critical
threshold.
, playing the role of a critical
threshold.
It turns out that the variational problem in (11) has a
minimiser for all
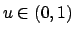 when
when
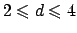 , but
only for
, but
only for
![$ u \in (0,u_d]$](img346.png) when
when
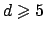 . The critical threshold
. The critical threshold
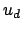 is associated with `leakage' in the variational problem. In
terms of the optimal strategy behind the moderate deviations, this
leakage is associated with a `collapse transition': the path spends
parts of its time on two different space scales.
is associated with `leakage' in the variational problem. In
terms of the optimal strategy behind the moderate deviations, this
leakage is associated with a `collapse transition': the path spends
parts of its time on two different space scales.
It is not known whether the minimiser is unique when it exists.
This seems to be a tough analytic problem. Very little is known
about the moderate deviations in the upward direction,
i.e., events
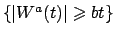 with
with
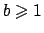 . These are
expected to behave completely differently.
. These are
expected to behave completely differently.
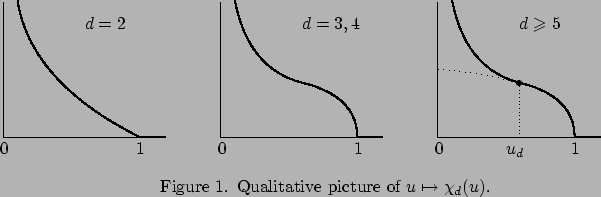


Next: References
Up: Fluctuations of the Wiener
Previous: Moderate deviations