Let
For instance, if
Let
We mention some recent developments in Diophantine geometry which are related to the results from the second section. This section is more specialized.
We write
![]() for the multiplicative group
for the multiplicative group
![]() with
coordinatewise
multiplication
with
coordinatewise
multiplication
![]() .
The group
.
The group
![]() is the group of complex points of a
group variety
is the group of complex points of a
group variety
![]() , called the
, called the ![]() -dimensional linear torus.
Lang ([14], p. 220)
proposed the following conjecture:
-dimensional linear torus.
Lang ([14], p. 220)
proposed the following conjecture:
Let ![]() be either
be either
![]() or an abelian variety defined over
or an abelian variety defined over
![]() .
Let
.
Let ![]() be a subgroup of
be a subgroup of
![]() of finite rank (i.e.,
of finite rank (i.e., ![]() has a
finitely
generated subgroup
has a
finitely
generated subgroup ![]() such that
such that
![]() is a torsion group).
Further, let
is a torsion group).
Further, let ![]() be an algebraic subvariety of
be an algebraic subvariety of ![]() defined over
defined over
![]() and let
and let
![]() denote the exceptional set of
denote the exceptional set of ![]() , that is the union of all
translates
of positive dimensional algebraic subgroups of
, that is the union of all
translates
of positive dimensional algebraic subgroups of ![]() which are contained
in
which are contained
in ![]() .
Then the intersection
.
Then the intersection
![]() is finite.
is finite.
For instance, if
![]() and
and ![]() is a hyperplane given by
is a hyperplane given by
![]() then
then
![]() is the set of solutions of
is the set of solutions of
![]() in
in
![]() , that is, we
have an equation
of type (2). The non-degenerate solutions of this equation
(i.e., with non-vanishing subsums) are precisely the points in
, that is, we
have an equation
of type (2). The non-degenerate solutions of this equation
(i.e., with non-vanishing subsums) are precisely the points in
![]() . So Lang's conjecture implies that
(2)
has only finitely many non-degenerate solutions.
. So Lang's conjecture implies that
(2)
has only finitely many non-degenerate solutions.
Let ![]() be a projective curve of genus
be a projective curve of genus
![]() defined over an algebraic number field
defined over an algebraic number field ![]() , let
, let ![]() be the Jacobian of
be the Jacobian of
![]() ,
and let
,
and let
![]() . We assume that
. We assume that
![]() . We know that
. We know that
![]() and that
and that ![]() is finitely generated (the Mordell-Weil Theorem).
Thus Lang's conjecture implies Mordell's conjecture that
is finitely generated (the Mordell-Weil Theorem).
Thus Lang's conjecture implies Mordell's conjecture that ![]() is
finite.
is
finite.
In the 1980's, Laurent [15] proved Lang's conjecture in the case
that
![]() . Laurent's proof was based on the p-adic Subspace Theorem.
In 1983, Faltings [9] proved Mordell's conjecture. Unlike
Laurent,
Faltings did not use Diophantine approximation. In 1991,
Vojta [29] gave a totally different proof of Mordell's
conjecture
based on Diophantine approximation.
Then by extending Vojta's ideas to
higher dimensions,
Faltings [10],[11]
achieved the following breakthrough, which almost settled Lang's
conjecture for
abelian varieties:
. Laurent's proof was based on the p-adic Subspace Theorem.
In 1983, Faltings [9] proved Mordell's conjecture. Unlike
Laurent,
Faltings did not use Diophantine approximation. In 1991,
Vojta [29] gave a totally different proof of Mordell's
conjecture
based on Diophantine approximation.
Then by extending Vojta's ideas to
higher dimensions,
Faltings [10],[11]
achieved the following breakthrough, which almost settled Lang's
conjecture for
abelian varieties:
Let ![]() be an abelian variety, and let
be an abelian variety, and let ![]() be a projective
subvariety of
be a projective
subvariety of ![]() , both defined over an algebraic number field
, both defined over an algebraic number field ![]() .
Then
.
Then
![]() is finite.
is finite.
Subsequently, the proof of Lang's conjecture was completed by McQuillan
[18]. We refer to the books [12], [2] for an
introduction.
Very recently, Rémond proved the following remarkable quantitative
version
of Lang's conjecture.
Rémond used Faltings' arguments,
but he managed to simplify them considerably.
If
![]() we assume that
we assume that
![]() by identifying
by identifying
![]() with the point
with the point
![]() .
if
.
if ![]() is an abelian variety we assume that
is an abelian variety we assume that
![]() is contained in some projective
space
is contained in some projective
space
![]() and that the line sheaf
and that the line sheaf ![]() is symmetric.
Further we assume that
is symmetric.
Further we assume that ![]() is defined over the field of algebraic
numbers.
In both cases,
is defined over the field of algebraic
numbers.
In both cases, ![]() has dimension
has dimension ![]() ,
, ![]() is an algebraic
subvariety of
is an algebraic
subvariety of ![]() of dimension
of dimension ![]() and degree
and degree ![]() (with respect to the
embeddings
chosen above) defined over the algebraic numbers,
and
(with respect to the
embeddings
chosen above) defined over the algebraic numbers,
and ![]() is a subgroup of
is a subgroup of
![]() of finite rank
of finite rank ![]() .
.
Theorem (Rémond).
(i) Let
![]() . Then
. Then
![]() has cardinality at
most
has cardinality at
most
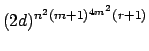 ([21]).
([21]).
(ii) Let ![]() be an abelian variety. Then
be an abelian variety. Then
![]() has cardinality at most
has cardinality at most
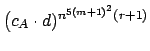 ,
where
,
where ![]() is an effectively computable constant depending on
is an effectively computable constant depending on ![]() ([19],[20]).
([19],[20]).