The parametrization of tempered representations
of
![]() can be reformulated as follows. We need to
introduce the Weil group
can be reformulated as follows. We need to
introduce the Weil group ![]() of
of ![]() .
This group is a non-split extension of
the multiplicative group
.
This group is a non-split extension of
the multiplicative group ![]() of
of ![]() by
by
![]() . Explicitly,
. Explicitly,
![]() ,
where
,
where ![]() and
and
![]() for
for
![]() .
An
.
An ![]() dimensional complex representation
dimensional complex representation ![]() of
of ![]() is
said to be admissible if
is
said to be admissible if ![]() is continuous and if
is continuous and if
![]() consists of semisimple matrices.
The local Langlands reciprocity conjecture for
consists of semisimple matrices.
The local Langlands reciprocity conjecture for
![]() (which is known to be true)
states that the irreducible admissible representations of
(which is known to be true)
states that the irreducible admissible representations of
![]() are in 1-1 correspondence with the admissible n-dimensional
representations of
are in 1-1 correspondence with the admissible n-dimensional
representations of ![]() . This parametrization respects classes
of representations with special properties. For instance,
the tempered representations correspond to
the unitary representations of
. This parametrization respects classes
of representations with special properties. For instance,
the tempered representations correspond to
the unitary representations of ![]() , and the discrete series
representations
correspond to the representations of
, and the discrete series
representations
correspond to the representations of ![]() whose image is not
contained in any proper parabolic subgroup (i.e. a subgroup containing
a conjugate of the subgroup of upper triangular matrices).
whose image is not
contained in any proper parabolic subgroup (i.e. a subgroup containing
a conjugate of the subgroup of upper triangular matrices).
For general real reductive groups2
![]() , Langlands has defined a dual reductive group
, Langlands has defined a dual reductive group ![]() (over
(over
![]() ) such that the conjugacy classes of admissible homomorphisms of
the group
) such that the conjugacy classes of admissible homomorphisms of
the group ![]() to
to ![]() should correspond to finite
``packets'' of ``L-indistinguishable'' irreducible admissible
representations. What controls the size of these
finite packets is not completely clear,
and this complicates the precise formulation of the
local Langlands correspondence in this generality considerably.
should correspond to finite
``packets'' of ``L-indistinguishable'' irreducible admissible
representations. What controls the size of these
finite packets is not completely clear,
and this complicates the precise formulation of the
local Langlands correspondence in this generality considerably.
As a simple example, let us look at the case
![]() . Its dual group is
. Its dual group is
![]() .
The unitary representations of
.
The unitary representations of ![]() are easily seen to be conjugate to precisely one of the
following
are easily seen to be conjugate to precisely one of the
following
(1)
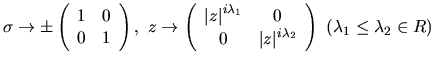
(2)
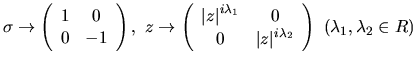
(3)
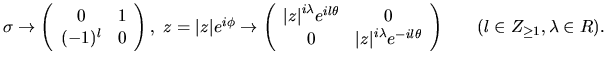
This list of possibilities corresponds nicely to the well known list of
irreducible tempered representations of
![]() .
The cases (1) and (2) correspond to spherical and non-spherical
unitary principal series, and (3) corresponds to the discrete
series.
.
The cases (1) and (2) correspond to spherical and non-spherical
unitary principal series, and (3) corresponds to the discrete
series.
The (slightly more complicated)
classification of unitary representations of
![]() was already
known since 1947, by a famous paper of Bargmann. The results for
was already
known since 1947, by a famous paper of Bargmann. The results for
![]() can be easily reconstructed from that paper.
The fact that the irreducible tempered representations of
can be easily reconstructed from that paper.
The fact that the irreducible tempered representations of
![]() are in correspondence with a list of equivalence classes of
continuous homomorphisms of
are in correspondence with a list of equivalence classes of
continuous homomorphisms of ![]() seems coincidental.
After all, the construction of
the various series of tempered representations and the proof of their
completeness, is a delicate and complicated analytic task. The
techniques and constructions that are employed have, at first sight,
nothing in common with the set of equivalence classes of
two dimensional unitary representations of
seems coincidental.
After all, the construction of
the various series of tempered representations and the proof of their
completeness, is a delicate and complicated analytic task. The
techniques and constructions that are employed have, at first sight,
nothing in common with the set of equivalence classes of
two dimensional unitary representations of ![]() .
.
Yet, in the 1960's Langlands has put forward his now famous reciprocity conjecture, asserting that
Langlands reciprocity conjecture was inspired by the famous
reciprocity law of Emil Artin.
Artin's reciprocity law states precisely that the
abelianized group ![]() is isomorphic to
is isomorphic to
![]() in the local case, and to the idele class group
in the local case, and to the idele class group
![]() in the global case.
We can restate this by saying that the unitary characters
of
in the global case.
We can restate this by saying that the unitary characters
of ![]() should correspond bijectively to
the unitary characters of
should correspond bijectively to
the unitary characters of ![]() (local case) or
to the unitary characters of the idele class group
(Hecke characters) (global case).
It is the case
(local case) or
to the unitary characters of the idele class group
(Hecke characters) (global case).
It is the case ![]() of the Langlands reciprocity
conjecture.
of the Langlands reciprocity
conjecture.
The conjecture has many refinements predicting how the correspondence
behaves under restriction to subclasses of representations, base
change, and most profoundly, homomorphisms between the dual groups
![]() (Langlands functoriality principle).
Even locally this predicts, in a very precise way,
properties of irreducible unitary representations.
(Langlands functoriality principle).
Even locally this predicts, in a very precise way,
properties of irreducible unitary representations.
Many special cases have been verified over the last three decades, but it is fair to say that it remains a mystery why it works.
Recently, the local Langlands correspondence for
![]() with
with ![]() a p-adic field was verified by
Harris and Taylor, and Henniart. The correspondence was also
verified for
a p-adic field was verified by
Harris and Taylor, and Henniart. The correspondence was also
verified for ![]() in the case of a global field of positive
characteristic (Drinfeld, Lafforgue).
Although these are certainly a very
important steps forward, the methods that have been used are not
applicable to the general reductive case.
in the case of a global field of positive
characteristic (Drinfeld, Lafforgue).
Although these are certainly a very
important steps forward, the methods that have been used are not
applicable to the general reductive case.