Conditioning on data

What one would like for practical purposes is that the simulations are conditioned on knowledge that is already available. In particular on information from well logs. Now as long as there is one well this is easily done in the way described before: simply use the information from the vertical⁵ well as initial states for the left hand column of the simulation to be generated (The states in the top row are obtainable too, as they describe the surface.) However, a particulary interesting situation is one where there is information from two wells. How is conditioning going to be performed in this case? Already in the one-dimensional case such a conditioning does not seem feasible at first sight: a Markov chain evolves typically from past to future so how can you correctly fill in the near future if you already know the far future? Actually it is mathematically very simple to accomplish this. Let $(X_n)^\infty_{n=0}$ be the chain of states at time $n=0,1,\dots$, and let $(P_{st})_{s,t \in S}$ be the matrix of transition probabilities, i.e., for all $s,t \in S$ and $n \ge 1$

$$P_{st}=\mathbb P(X_{n+1}=t\vert\,X_n=s)$$

Furthermore let $P^{(n)}=P^n$ be the matrix of $n$-step transition probabilities. Suppose we are given time instants $n,n+1$ and $N > n+1$ (the far future). Then a simple calculation shows that

$$\mathbb P(X_{n+1}=t\vert\,X_n=s,X_N=u) = \frac{P_{st}P_{tu}^{(N-n-1)}}{P^{(N-n)}_{su}}.$$

0.8Fig2.eps

Figure 2. Top: the target reservoir. Left: well log information (2,3,5 and 7 wells. Right: simulated reservoirs conditioned on well logs.

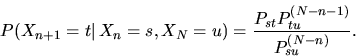
This formula yields a cheap way to generate Markov chain realisations conditioned on the future. The two-dimensional case is much more complicated, it is even not clear what ``future'' means in that case. In the geological application it is however clear where one wants to condition on: the left most column, and the right most column which represent data from two wells. In our paper an ``engineering'' solution has been chosen to the conditioning problem: the horizontal chain is conditioned as described above, and then this conditioned chain is coupled to the vertical chain. For exact conditioning it is useful to note (see also Galbraith and Walley) that a unilateral Markov random field can also be described by a one-dimensional Markov chain in a random environment (the random environment is generated by the chain itself). In fact, define for $r \in S$ the matrix $P^{[r]}$ by

$$P^{[r]}_{st} = \mathbb P(Z_{m+1,n}=t\vert\,Z_{mn}=s,Z_{m+1,n-1}=r), \;\;\; s,t \in S.$$

Then the following holds for $M \ge 1$

$$\begin{eqnarray*} && \mathbb P(Z_{m+M,n}=t\vert\,Z_{m,n}=s, Z_{m+1,n-1}=r_1,\dot... ...{m+M,n-1}=r_M)\\ && = (P^{[r_1]}P^{[r_2]} \dots P^{[r_M]})_{st}. \end{eqnarray*}$$

Now if we define the future of $(m,n)$ to be $(M,n)$, where $M$ is the index of the right most column, then we obtain similarly to the computation for the one dimensional case

$$\begin{eqnarray*} && \mathbb P(Z_{m+1,n}=t\vert\,Z_{mn}=s, Z_{m+1,n-1}=r_1, \dot... ... P^{[r_{M-n+1}]})_{tu}}{(P^{[r_1]} \dots P^{[r_{M-n+1}]})_{su}}. \end{eqnarray*}$$

It is clear that this exact conditioning is computationally much more expensive. See Figure 2 for simulations with this model using the approximative (cheap) conditioning mentioned earlier. The perceptive reader will note that there are still some unwanted effects in the results.