The type of investigations described above are also applied to analyse the dynamics of a Hopfield model for neural networks in [8].
The Hopfield model is the following neural network model for associative memory. We are given N neurons, each of which can be in state 0 or 1. We assume that the memory contains a given set of p images. At time t neuron i is selected with probability 1/N, and the new state of this neuron is determined according to conditional Gibbs probabilities with a given energy function, which we will not further specify. We consider only the zero temperature dynamics and then the new state of the neuron is deterministic and such that the energy of the new configuration does not increase. In our paper the energy function assigns lowest energy to the images themselves and so one expects that with probability 1 one of the images from memory is retrieved. This is not true: not only images where the energy has a global minimum, but also images where the energy has a local minimum can be retrieved. It is a well-known fact that global/local minima correspond to fixed points of the limiting dynamics.
Most research on this model (cf. for example [1]) deals with the domains of attraction
of these fixed points, when the number of images grows
in some prespecified way with the number of neurons N.
Almost no results exist on the exact form of the dynamics in the thermodynamic limit
. Nevertheless, to understand the quality of the model,
the limiting dynamics are an important tool. It will give insight
into questions like whether from any input image one of the
images from memory are retrieved and how long it will take.
For analysing this problem we needed to reformulate the model as a Markov chain on a state space with a dimension independent of N. By using the commonly used overlap representation the Markov property gets lost and the understanding of the limiting dynamics becomes more complicated. Clearly, the obtained Markov chain still depends on N and the jump probabilities depend more strongly on the initial state than in the rw case. Therefore, for determining the limiting dynamics of the same time-space scaled process as above, a more general version of the LLN was required.
A surprising result was the existence of ``traps'': these are not fixed points, but nevertheless can be limit points of the limiting dynamics. Since non-trivial examples only occur in dimension at least 8, we show a generic example of the limiting dynamics in Figure 4: to each region corresponds a quasi-attractor attracting all images from this region. Hence an image is successively attracted by different quasi-attractors till it reaches a fixed point (A) or a ``trap'' (B).
=.5mm
0.4pt
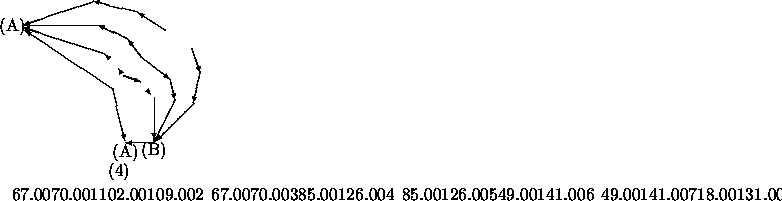
Contrary to the random walk case where the ``speed'' along Euler paths is piecewise constant, the speed decreases exponentially while approaching the quasi-attractor. A trap is therefore never reached, although it is left immediately when it is reached. Translated back to the original system, it means that fixed points or traps are reached at a speed that is slower than linear in N.
The picture also shows the occurrence of scattering. Moreover, we have been able to prove that the limiting dynamics are acyclic and so bouncing back and forth between different quasi-attractors cannot happen.
The described analysis is a first start in my research in neural networks, which has been conducted the past year. The investigation of more complicated problems will be the next step. These problems concern the finite temperature dynamics; the number of fixed points; the question whether the time to reach an epsilon-distance of a local/global minimum or trap is uniformly bounded in the number of images; the dynamics when the number of images grows with the number of neurons.