

Next: Strong law and central
Up: Fluctuations of the Wiener
Previous: Fluctuations of the Wiener
Let  ,
,
 , be the standard Brownian motion in
, be the standard Brownian motion in
 (the Markov process with generator
(the Markov process with generator  )
starting at 0. Let
)
starting at 0. Let  denote its probability law and
expectation on path space. The Wiener sausage with radius
denote its probability law and
expectation on path space. The Wiener sausage with radius
 is the process defined by
is the process defined by
 (1)
(1)
where  is the open ball with radius
is the open ball with radius 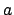 around
around
 ,
i.e.,
,
i.e.,  is the
is the 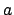 -environment of the
Brownian path up to time
-environment of the
Brownian path up to time  . The Wiener sausage is an important
mathematical object, because it is one of the simplest examples
of a non-Markovian functional of Brownian motion. It plays a key
role in the study of various stochastic phenomena, such as heat
conduction and trapping in random media, as well as in the
analysis of spectral properties of random Schrödinger operators.
. The Wiener sausage is an important
mathematical object, because it is one of the simplest examples
of a non-Markovian functional of Brownian motion. It plays a key
role in the study of various stochastic phenomena, such as heat
conduction and trapping in random media, as well as in the
analysis of spectral properties of random Schrödinger operators.