

Next: Moderate deviations
Up: Fluctuations of the Wiener
Previous: Strong law and central
The large deviation properties of  in the downward
direction have been studied by Donsker and Varadhan [3],
Bolthausen [2] and Sznitman [7]. For
in the downward
direction have been studied by Donsker and Varadhan [3],
Bolthausen [2] and Sznitman [7]. For
 the
outcome, proved in successive stages of refinement, reads as follows:
the
outcome, proved in successive stages of refinement, reads as follows:
 (4)
(4)
for any
 satisfying
satisfying
 and
and
 (5)
(5)
where
 is the smallest Dirichlet eigenvalue of
is the smallest Dirichlet eigenvalue of  on
the ball with unit volume. It turns out that the optimal strategy
for the Brownian motion to realise the large deviation in (4)
is to explore a ball with volume
on
the ball with unit volume. It turns out that the optimal strategy
for the Brownian motion to realise the large deviation in (4)
is to explore a ball with volume  until time
until time  , i.e., the
Wiener sausage covers this ball entirely and nothing outside. This
optimal strategy is simple and its optimality comes from the Faber-Krahn
isoperimetric inequality.
, i.e., the
Wiener sausage covers this ball entirely and nothing outside. This
optimal strategy is simple and its optimality comes from the Faber-Krahn
isoperimetric inequality.
Note that, apparently, a deviation below the scale of the mean
`squeezes all the empty space out of the Wiener sausage'. Also note
that the limit in (4) does not depend on 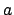 .
.
 (5)
(5)