References

[1] A. V. ARHANGEL'SKI, On linear homeomorphisms of function spaces, Soviet Math. Doklady 25 (1982), 852-855.

[2] A. V. ARHANGELSKI, A survey of $C_p$-theory, Questions and Answers, Gen. Top. 5 (1987), 1-109.

[3] A. V. ARHANGELSKI, Topological function spaces, Math. Appl., vol. 78, Kluwer Academic Publishers, Dordrecht, 1992.

[4] A. V. ARHANGELSKI, Some observations on $C_p$-theory and bibliography, Top. Appl. 89 (1998), 203-221.

[5] J. BAARS, H. GLADDINES, AND J. VAN MILL, Absorbing systems in infinite-dimensional manifolds, Top. Appl. 50 (1993), 147-182.

[6] J. BAARS AND J. DE GROOT, On topological and linear equivalence of certain function spaces, CWI Tract, vol. 86, Centre for Mathematics and Computer Science, Amsterdam, 1990

[7] J. BAARS, J. DE GROOT, AND J. PELANT, Function spaces of completely metrizable spaces, Trans. Amer. Math. Soc. 340 (1993), 871-879.

[8] C. BESSAGA AND A. PECZY´NSKI, Spaces of continuous functions ${I}{V}$ (on isomorphical classification of spaces of continuous functions), Studia Math. 19 (1960), 53-62.

[9] M. BESTVINA AND J. MOGILSKI, Characterizing certain incomplete infinite-dimensional absolute retracts, Michigan Math. J. 33 (1986), 291-313.

[10] J. CALBRIX, Classes de Baire et espaces d'applications continues, C. R. Acad. Sci. Paris 301 (1985), 759-762.

[11] J. CALBRIX, Filtres Boréliens sur l'ensemble des entiers et espaces des applications continues, Rev. Roumaine Math. Pure Appl. 33 (1988), 655-661.

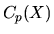
[12] R. CAUTY, La classe Borélienne ne détermine pas le type topologique de $C_p(X)$, Serdica Math. J. 24 (1998), 307-318.

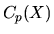
[13] R. CAUTY, T. DOBROWOLSKI, AND W. MARCISZEWSKI, A contribution to the topological classification of the spaces $C_p(X)$, Fund. Math. 142 (1993), 269-301.

[14] J. DIJKSTRA, T. GRILLIOT, J. VAN MILL, AND D. J. LUTZER, Function spaces of low Borel complexity, Proc. Amer. Math. Soc. 94 (1985), 703-710.

[15] J. DIJKSTRA AND J. MOGILSKI, The ambient homeomorphy of certain function and sequence spaces, Comm. Math. Univ. Carolinae 37 (1996), 595-611.

[16] T. DOBROWOLSKI, W. MARCISZEWSKI, AND J. MOGILSKI, On topological classification of function spaces ${C}_{p}({X})$ of low Borel complexity, Trans. Amer. Math. Soc. 678 (1991), 307-324.

[17] J. DUGUNDJI, Topology, Allyn and Bacon, Boston, 1966.

[18] I. M. GELFAND AND A. N. KOLMOGOROFF, On rings of continuous functions on topological spaces, Comptes Rendus (Doklady) de l'Académie des Sciences de l'URSS 22 (1939), 11-15.

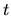
[19] S. P. GUL'KO AND T. E. KHMYLEVA, Compactness is not preserved by $t$-equivalence, Mat. Zametki 39 (1986), 895-903, in Russian.

[20] D. J. LUTZER AND R. MCCOY, Category in function spaces. I, Pac. J. Math. 90 (1980), 145-168.

[21] D. J. LUTZER, J. VAN MILL, AND R. POL, Descriptive complexity of function spaces, Trans. Amer. Math. Soc. 291 (1985), 121-128.

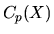
[22] W. MARCISZEWSKI, A function space $C_p(X)$ not linearly homeomorphic to $C_p(X)\times {\mathbb R}$, Fund. Math. 153 (1997), 125-140.

[23] R. A. MCCOY AND I. NTANTU, Topological properties of spaces of continuous functions, Lecture Notes in Mathematics, vol. 1315, Springer-Verlag, 1988.

[24] A. A. MILJUTIN, Isomorphisms of the spaces of continuous functions over compact sets of the cardinality of the continuum, Teor. Funkcii Funk cional Anal i Prilozen (in Russian) (Kharkov) 2 (1966), 150-156.

[25] J. VAN MILL, Topological equivalence of certain function spaces, Compositio Math. 63 (1987), 159-188.

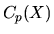
[26] J. VAN MILL, $C_p(X)$ is not $G_{\delta\sigma}$: a simple proof, Bull. Polon. Acad. Sci. Sér. Math. Astronom. Phys. 47 (1999), 319-323.

[27] J. NAGATA, On lattices of functions on topological spaces and functions on uniform spaces, Osaka Math. J. 1 (1949), 166-181.

[28] V. G. PESTOV, The coincidence of the dimension $\dim$ of $l$-equivalent topological spaces, Soviet Math. Doklady 26 (1982), 380-383.