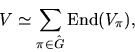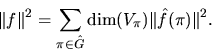Next: Locally compact groups
Up: Representation Theory of Algebraic
Previous: Representation Theory of Algebraic
At the end of the nineteenth century
Frobenius started the systematic study of complex
representations of finite groups. He defined the notion of
a group representation, and studied the representations of
important groups such as 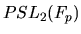 , the symmetric groups
, the symmetric groups
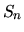 and the alternating groups
and the alternating groups 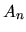 .
In modern terminology, a (complex) representation of a finite group
.
In modern terminology, a (complex) representation of a finite group
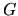 is a group homomorphism
is a group homomorphism
where 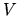 is a complex vector space.
The representation is called irreducible if
is a complex vector space.
The representation is called irreducible if 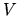 has no subspaces
other than
has no subspaces
other than 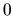 or
or 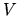 that are invariant under
that are invariant under 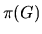 . Two
representations
. Two
representations 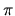 and
and 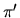 of
of 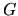 are called
equivalent if there exists a
linear isomorphism
are called
equivalent if there exists a
linear isomorphism
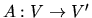 such that
such that 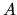 is
is 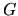 -equivariant,
i.e.
-equivariant,
i.e.
In general, linear maps 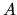 that satisfy this equation
are called
that satisfy this equation
are called 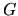 -maps or intertwiners.
The investigation of
representations of general finite groups was soon picked up by Burnside,
Schur, and many others. The main results of their work can be
formulated as follows:
-maps or intertwiners.
The investigation of
representations of general finite groups was soon picked up by Burnside,
Schur, and many others. The main results of their work can be
formulated as follows:
- (1)
- Every representation of a finite group is
unitarizable. This means that there exists a Hilbert space structure
on
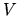 such that
such that
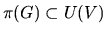 .
.
- (2)
- Consequently, every representation of
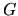 is equivalent
to a direct sum of irreducible representations.
is equivalent
to a direct sum of irreducible representations.
- (3)
- (Schur's lemma) When
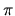 and
and 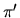 are
irreducible and inequivalent, the only intertwiner
are
irreducible and inequivalent, the only intertwiner 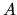 between
between 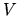 and
and 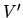 is
is 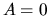 . On the other hand, when
. On the other hand, when
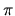 and
and 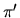 are equivalent, every nonzero intertwiner
are equivalent, every nonzero intertwiner 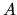 is an isomorphism. In particular, when
is an isomorphism. In particular, when
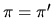 every
intertwiner is scalar.
every
intertwiner is scalar.
- (4)
- By (3), the decomposition in (2) is essentially
unique.
- (5)
- The left regular representation of
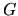 is defined by the
left multiplication of
is defined by the
left multiplication of 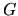 on itself. More precisely, we take
on itself. More precisely, we take 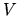 as the space of complex valued functions on
as the space of complex valued functions on 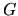 , and define the
left regular representation
, and define the
left regular representation 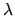 by
by
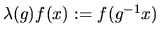 .
Similarly, we define the right regular representation
.
Similarly, we define the right regular representation 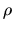 on
on 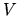 by the right multiplication of
by the right multiplication of 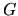 on itself.
Then
on itself.
Then 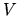 is a
is a 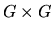 representation via
representation via
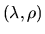 .
As such,
.
As such, 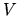 is equivalent to the direct sum
is equivalent to the direct sum
where 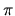 runs over the set
runs over the set 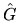 of all equivalence classes of irreducible
representations of
of all equivalence classes of irreducible
representations of 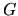 .
.
- (6)
- (Plancherel formula) If
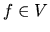 , we define
its Fourier transform
, we define
its Fourier transform 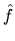 as the function on
as the function on
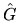 such that
such that
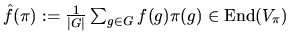 .
We give
.
We give 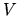 a Hilbert space structure by the Hermitian
inner product
a Hilbert space structure by the Hermitian
inner product
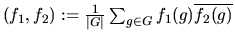 . Then
. Then
Here
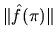 denotes the Hilbert-Schmidt norm
of
denotes the Hilbert-Schmidt norm
of
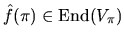 .
.



Next: Locally compact groups
Up: Representation Theory of Algebraic
Previous: Representation Theory of Algebraic
![]() that satisfy this equation
are called
that satisfy this equation
are called ![]() -maps or intertwiners.
The investigation of
representations of general finite groups was soon picked up by Burnside,
Schur, and many others. The main results of their work can be
formulated as follows:
-maps or intertwiners.
The investigation of
representations of general finite groups was soon picked up by Burnside,
Schur, and many others. The main results of their work can be
formulated as follows: