


Next: References
Up: Representation Theory of Algebraic
Previous: Langlands reciprocity
For general p-adic reductive groups the local Langlands correspondence
is much more complicated than the case 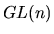 .
We have been working on the verification of the Langlands conjecture
for so called level 1 representations of simple split forms
.
We have been working on the verification of the Langlands conjecture
for so called level 1 representations of simple split forms
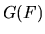 . Lusztig [5] has given a conjectural form of the Langlands
conjecture at this level for the most complicated class of singular
representations, the so called unipotent representations. It is not
clear at present whether Lusztig's version of the correspondence has the
expected behavior with respect to natural partitions of the
set of unipotent representations.
To understand such questions we have to study the properties of
unipotent representations.
The methods that we use are based on Lusztig's
theorem that the centralizer algebras of representations that are
induced from cuspidal unipotent representations are affine Hecke
algebras. We can therefore deduce many properties of unipotent
representations by the analytic study of affine Hecke algebras.
We study the Hecke algebras from the point of view of
. Lusztig [5] has given a conjectural form of the Langlands
conjecture at this level for the most complicated class of singular
representations, the so called unipotent representations. It is not
clear at present whether Lusztig's version of the correspondence has the
expected behavior with respect to natural partitions of the
set of unipotent representations.
To understand such questions we have to study the properties of
unipotent representations.
The methods that we use are based on Lusztig's
theorem that the centralizer algebras of representations that are
induced from cuspidal unipotent representations are affine Hecke
algebras. We can therefore deduce many properties of unipotent
representations by the analytic study of affine Hecke algebras.
We study the Hecke algebras from the point of view of  -algebras,
and this seems to be a fruitful approach.
Some of the ideas leading to this approach come from
new constructions of Hecke algebras, due to Ivan Cherednik (North
Carolina). The origin of these constructions can be traced back to
conformal field theory.
-algebras,
and this seems to be a fruitful approach.
Some of the ideas leading to this approach come from
new constructions of Hecke algebras, due to Ivan Cherednik (North
Carolina). The origin of these constructions can be traced back to
conformal field theory.
This work has led to a satisfactory description of the L-packets of
unipotent representations for exceptional groups,
and of the formal degrees of their cuspidal unipotent
representations. These developments also have an impact on
the theory of representations finite simple groups of Lie type.
For example, it was shown that the dimension of a unipotent
cuspidal representation
of a simple group of Lie type is given by a formula
resembling the famous Weyl character formula.
Part of this work was done in collaboration with Gerrit Heckman
(Nijmegen) [3] and Mark Reeder (Boston college) [7].
The research group of Van Dijk (Leiden) studies the
harmonic analysis on homogeneous spaces of real reductive groups.
This topic is closely related to the research described above.
There is also a natural connection with the research in quantum groups and
special functions by Koornwinder (UVA) and his group, and
the research in operator algebra theory by Landsman (UVA).
The references [1], [2], [4] may serve as a good starting
point for further reading.



Next: References
Up: Representation Theory of Algebraic
Previous: Langlands reciprocity