


Next: Topological equivalence of function
Up: Preliminaries
Previous: - and -equivalence
With the operations of pointwise addition and pointwise
multiplication, 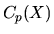 is a commutative topological ring with
unit, the unit being the constant function with value 1. It is
a
famous theorem of Gel
is a commutative topological ring with
unit, the unit being the constant function with value 1. It is
a
famous theorem of Gel fand and
Kolmogoroff [18] that the
ring structure by itself determines the topological structure on
fand and
Kolmogoroff [18] that the
ring structure by itself determines the topological structure on
 provided
provided  is compact. They proved that if
is compact. They proved that if  and
and  are
compact and
are
compact and  and
and  are isomorphic as rings then
are isomorphic as rings then  and
and
 are homeomorphic. For details,
see also Dugundji [17, Theorem XIII.6.5].
(The proof in [17] makes use of the
topology of pointwise convergence.)
are homeomorphic. For details,
see also Dugundji [17, Theorem XIII.6.5].
(The proof in [17] makes use of the
topology of pointwise convergence.)
For noncompact spaces  , the algebraic structure of
, the algebraic structure of  is,
in general, not strong enough to determine the topology of
is,
in general, not strong enough to determine the topology of  .
For consider the spaces
.
For consider the spaces  and
and  . Then
clearly
. Then
clearly  and
and  are isomorphic as rings, but
are isomorphic as rings, but  and
and  are not homeomorphic.
are not homeomorphic.
For arbitrary spaces there is a result in the same spirit though.
Nagata [27]proved that 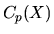 and
and  are topologically isomorphic as topological rings if and
only if
are topologically isomorphic as topological rings if and
only if  and
and  are homeomorphic. That we deal with real
valued functions is essential in this result. It
was shown in Arhangel
are homeomorphic. That we deal with real
valued functions is essential in this result. It
was shown in Arhangel ski
ski [3, page 12]
that the ring of all continuous functions
[3, page 12]
that the ring of all continuous functions
 ,
endowed with the topology of pointwise convergence, does not
always determine the topological type of
,
endowed with the topology of pointwise convergence, does not
always determine the topological type of  .
.



Next: Topological equivalence of function
Up: Preliminaries
Previous: - and -equivalence
![]() , the algebraic structure of
, the algebraic structure of ![]() is,
in general, not strong enough to determine the topology of
is,
in general, not strong enough to determine the topology of ![]() .
For consider the spaces
.
For consider the spaces ![]() and
and ![]() . Then
clearly
. Then
clearly ![]() and
and ![]() are isomorphic as rings, but
are isomorphic as rings, but ![]() and
and ![]() are not homeomorphic.
are not homeomorphic.
![]() and
and ![]() are topologically isomorphic as topological rings if and
only if
are topologically isomorphic as topological rings if and
only if ![]() and
and ![]() are homeomorphic. That we deal with real
valued functions is essential in this result. It
was shown in Arhangel
are homeomorphic. That we deal with real
valued functions is essential in this result. It
was shown in Arhangel![]() ski
ski![]() [3, page 12]
that the ring of all continuous functions
[3, page 12]
that the ring of all continuous functions
![]() ,
endowed with the topology of pointwise convergence, does not
always determine the topological type of
,
endowed with the topology of pointwise convergence, does not
always determine the topological type of ![]() .
.