


Next: Le cours de Jean
Up: Cours de DEA niveau
Previous: Cours de DEA niveau
Sous-sections
Le cours de Paul Baird (Université de Brest):
Théorie géométrique de mesure
Une motivation pour le développement de la théorie géométrique de
mesure est le problème de Plateau:
Donné une (n-1)-sous-variété orientée M dans 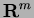 ,
trouver une sous-variété orientée N de dimension n minimisant
l'aire telle que
,
trouver une sous-variété orientée N de dimension n minimisant
l'aire telle que
 .
.
Exemples: (i) Soit M le graphe d'une fonction
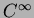 ,
,
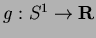 ; soit N le graphe d'une fonction
; soit N le graphe d'une fonction
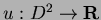 qui est solution du problème de Dirichlet:
qui est solution du problème de Dirichlet:
sur D2 et u = g sur
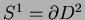 .
.
(ii) Soit
L'ensemble N de l'exemple (ii) est singulier en (0,0). Donc la
solution n'est pas toujours une sous-variété. Pourtant, en considérant
la limite d'une suite minimisante des sous-variétés, Federer et Fleming
ont introduit la notion de ``rectifiable current'', qu'on discutera dans
la 2ème partie du cours.
En général, la théorie géométrique de mesure est la théorie des
sous-variétés singulières dans 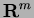 .
Elle applique des
notions de la théorie de mesures aux problèmes de la géométrie
différentielle. L'objectif est d'obtenir des résultats d'existence et de
régularité.
.
Elle applique des
notions de la théorie de mesures aux problèmes de la géométrie
différentielle. L'objectif est d'obtenir des résultats d'existence et de
régularité.
- 1.
- PARTIE ANALYTIQUE
- (a)
- Notion élémentaire de mesure: mesure de Borel, fonction
mesurable, mesure de Hausdorff.
- (b)
- Applications de Lipschitz: fonction différentiable, Théorème de
Radamacher, aire et co-aire des applications de Lipschitz.
- 2.
- PARTIE GEOMETRIQUE
- (a)
- Formes et courants : ensemble dénombrablement réctifiable,
l'espace tangent approximatif, courants dans
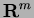 ,
masse,
théorèmes de déformation, de rectafiabilité et de compacité.
,
masse,
théorèmes de déformation, de rectafiabilité et de compacité.
- (b)
- Minimisation de masse : existence et régularité des courants
qui minimisent masse, cones minimisants et le problème de Bernstein.
- 1.
- H. Federer and W. Fleming, Normal and integral currents,
Annals of Math. 72 (1960), 458-520.
- 2.
- 2. H. Federer, Geometric measure theory, Springer-Verlag, 1969.
- 3.
- 3. E. Bombieri, E. De Giorgi and E. Giusti, Minimal cones and the
Bernstein problem, Invent. Math. 7 (1969), 243-268.
- 4.
- 4. R. Hardt, An introduction to geometric measure theory,
Lecture Notes, Melbourne University (1979).
Aucun sauf une connaissance des notions élémentaires des
sous-variétés dans 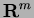 .
.
Les lundi 29 mai et 5 juin 2000 de 13h45 à 14h45
et de 15h à 16h, et les mardis 30 mai et 6 juin 2000, de 8h45 à
10h15 et de 10h45 à 12h15, + 5 autres heures precisées
ultérieurement. Lieu : salle 006 du batiment 22.



Next: Le cours de Jean
Up: Cours de DEA niveau
Previous: Cours de DEA niveau
Bas Edixhoven
2000-05-26
, trouver une sous-variété orientée N de dimension n minimisant l'aire telle que
.
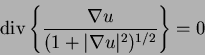
![]() .
Elle applique des
notions de la théorie de mesures aux problèmes de la géométrie
différentielle. L'objectif est d'obtenir des résultats d'existence et de
régularité.
.
Elle applique des
notions de la théorie de mesures aux problèmes de la géométrie
différentielle. L'objectif est d'obtenir des résultats d'existence et de
régularité.